Chapter 03. 회귀 알고리즘과 모델 규제

03-1. KNN 회귀

• 회귀? -> 변수 사이의 상관관계를 분석해 임의의 어떤 숫자를 예측
• KNN 회귀 : 근접한 이웃 k개의 타깃값의 평균으로 예측 타깃값을 결정

KNeighborsRegressor : KNN 회귀 모델을 만드는 scikit-learn 클래스

** numpy reshape : 배열의 크기를 바꿀 때 사용하는 method, 원본 배열에 있는 원소의 개수를 맞춰야함

test_array=np.array([1,2,3,4])
test_array=test_array.reshape(2,2) #(4,) --> (2,2)

• 결정계수($R^2$) -> KNN 분류에서 score = 정확하게 분류한 개수의 비율 -> 회귀의 경우 score = 결정계수($R^2$)로 판단

$R^2 = 1 - (타깃-예측)^2/(타깃-평균)^2$

• • mean_absolute_error : 타깃과 에측의 절댓값 오차를 평균하여 반환

from sklearn.metrics import mean_absolute_error
 test_prediction = knr.predict(test_input)
 mae = mean_absolute_error(test_target, test_prediction)

• 과대적합(overfitting) : 모델의 훈련 세트 성능이 테스트 세트 성능보다 너무 좋아서 데이터에 내재된 거시적인 패턴을 감지하지 못함
• 과소적합(underfitting) : 훈련 세트와 테스트 세트 성능이 모두 낮거나 테스트 세트 성능이 오히려 더 높아서 모델이 적절히 훈련되지 못함 ** 과소적합 해결방법 : 더 복잡한 모델을 사용해야함( ex - knn에서 k의 개수를 줄임)

03-2. 선형 회귀

• 선형 회귀 : 특성과 타깃 사의의 관계를 가장 잘 나타내는 선형 방정식을 찾음. 특성이 하나면 직석 방정식이 하나.

LinearRegression : 선형 회귀 모델을 만드는 scikit-learn 클래스

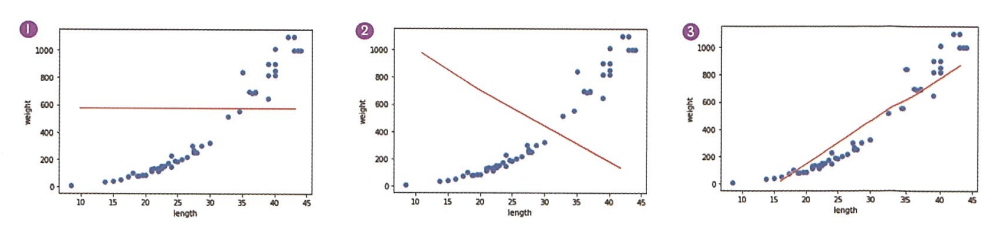
그래프 1. 데이터를 하나로 예측 -> 직선의 위치가 훈련 세트의 평균이라면 $R^2=0$ 그래프 2. 완전히 반대로 예측 -> $R^2<0$ 그래프 3. 가장 잘 예측한 직선 -> $R^2$이 1에 가까운 값

• 계수, 가중치 : 선형 회귀가 찾은 특성과 타깃 사이의 관계는 선형 방정식의 계수 또는 가중치에 저장됨. 보통 가중치는 방정식의 기울기를, 절편은 bias를 의미함

print(lr.coef_, lr.intercept_) # 기울기(특성의 계수)와 절편 확인

• 다항 회귀 : 다항식을 사용하여 특성과 타깃 사의의 관계 확인. 곡선처럼 비선형일 수 있지만 여전히 선형 회귀로 표현할 수 있음.